Skip to main content

5.9.2 Negativ binomial

Kommandoen som benyttes for å kjøre en Negativ binomialanalyse er negative-binomial.

Den første variabelen i lista er den avhengige variabelen (tellevariabel som teller opp forekomster av en gitt hendelse). Øvrige variabler (forklaringsvariabler) kan spesifiseres på samme måte som ved OLS (jfr. kommandoen regress).

Tilgjengelige opsjoner:

  • noconstant: Undertrykker konstantleddet

  • level(): Endre fra standard 95% konfidensintervall

  • robust: Robuste standardfeil

  • cluster(): Benytte clustervariabel (kan ikke benyttes sammen med robust)

  • control(): Ikke vis koeffisientestimater for utvalgte variabler

  • irr: Rapporterer incidence rate ratio-verdier i stedet for koeffisientverdier (verdiene transformeres gjennom den naturlige eksponensialfunksjonen). Verdien 1 betyr ingen effekt. Verdier over 1 betyr positiv effekt, mens verdier under 1 betyr negativ effekt.

  • exposure(): Inkluderer eksponeringsvariabel (kategorisk variabel). Denne representerer "mengden" av eksponering for den prosessen som genererer tellinger. Variabelen som angis inni parentesen må være kategorisk og må ikke inneholde 0-verdier. For eksempel, hvis du modellerer antallet bilulykker i forskjellige byer, kan tilknytning til by være en eksponeringsvariabel. Eksponeringsvariabelen blir automatisk log-transformert (naturlig logaritme) og inkludert som en offset i modellen, noe som betyr at den vil justere tellingsresponsen for mengden av eksponering. De andre estimatene blir da korrigert basert på denne variabelen, slik at de blir mer riktige. Merk at exposure-variabelen ikke skal angis som forklaringsvariabel i modellen.

Faktorvariabler, og cluster- og robust-estimering kan også benyttes. Fremgangsmåten er den samme som for ordinær lineær regresjon. Se hhv. kapittel 5.4.1 og 5.4.3 for mer informasjon om dette. For full oversikt over muligheter, bruk kommandoen help negative-binomial.

Eksempel på Negativ binomial-regresjon:

VIKTIG

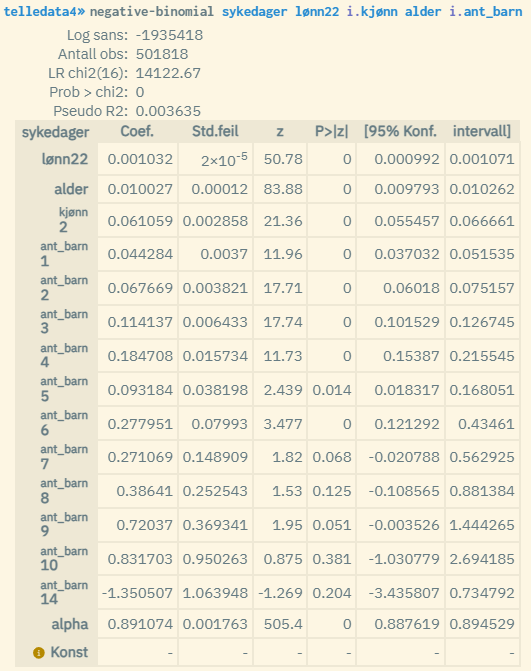
Merk at implementeringen av telleregresjonen Negativ binomial i microdata.no ikke er kompatibel med statistiske modeller der minst en av forklaringsvariablene har for høy verdi (dette vil typisk gjelde inntektsvariabler). Det anbefales å transformere verdiene til de aktuelle variablene slik at de kommer under en grenseverdi på ca. 400 (dette kan gjøres gjennom å dividere på en faktor eller bruke f.eks. en logaritmetransformasjon). Om ikke dette gjøres risikerer du å få et resultat som bare viser tomme verdier. Men så lenge det rapporteres estimater for alle forklaringsvariablene, så trenger du ikke foreta noen transformasjon.

Negativ binomial vs. Poisson​

Forskjellen mellom en Poissonregresjon og en Negativ binomial-regresjon er at i sistnevnte inngår parameteren alpha som skal fange opp ekstra varians (overdispersjon), og verdien på denne rapporteres nederst i listen over koeffisientestimater (over konstantleddet). Parameteren brukes altså til å skalere variansen til modellen1.

En alphaverdi på 0 innebærer at modellen er identisk med en Poissonmodell der varians = gjennomsnitt for responsvariabelen, og at en Poissonregresjon er mer passende å bruke. Positive alphaverdier tyder på overdispersjon (større spredning), og jo høyere verdi, dess større spredning. I eksempelet over er verdien 0.89. Dette tyder på at det er relativt stor grad av overdispersjon og at Negativ binomial-regresjon muligens er best å bruke (selv om Pseudo R2 har lavere verdi i forhold til Poisson).

Kilde:

Algoritmene for kommandoen negative-binomial baserer seg på funksjonen NegativeBinomial som man finner i Statsmodels-modulen i Python.


Fotnote:

Footnotes​

  1. Variansen til en Negativ binomialmodell kan uttrykkes slik: Varians = μ + α * μ2 , der μ = snitt av Y, α = alpha. I en Poissonmodell er alpha lik 0 slik at varians = snitt. ↩