5.4 Regress - ordinær lineær regresjonsanalyse
Kommandoen regress brukes til å utføre en ordinær lineær regresjonsanalyse (OLS) der den avhengige variabelen er en kontinuerlig/metrisk variabel. Et typisk eksempel er inntekt.
Syntax:
regress <variabel> <variabelliste> [if <betingelse>] [,<opsjoner>]
Den avhengige variabelen må angis først, etterfulgt av
forklaringsvariablene. Opsjoner kan benyttes for ulike formål, som f.eks. robust- eller cluster-estimering, jfr. underkapitlene nedenfor. I likhet med andre statistiske kommandoer, kan også regresjonskommandoer kombineres med en if-betingelse for å kjøre regresjoner på utvalgte grupper. For full oversikt over muligheter, bruk kommandoen help regress.
Kort fortalt går modellen ut på å estimere (mulige) marginaleffekter av et sett med uavhengige variabler (forklaringsvariabler) på den avhengige variabelen (responsvariabelen). Marginaleffekt er et mål på hvor mye den avhengige variabelen estimeres til å øke i verdi dersom en uavhengig variabel øker med én måleenhet.
Det viktigste å se på når en skal tolke resultatet av en regresjonskjøring er forklaringskraften til:
a) Modellen som helhet
b) Hver enkelt variabel
Dette gjøres ved å studere de respektive signifikansverdiene "Justert R2" og "P > |t|".
Nedenfor vises et eksempel på resultatet av en regresjonskjøring i microdata.no. Tallene i den nederste delen knyttes til de ulike variablene, mens tallene øverst viser til analysemodellen som helhet.
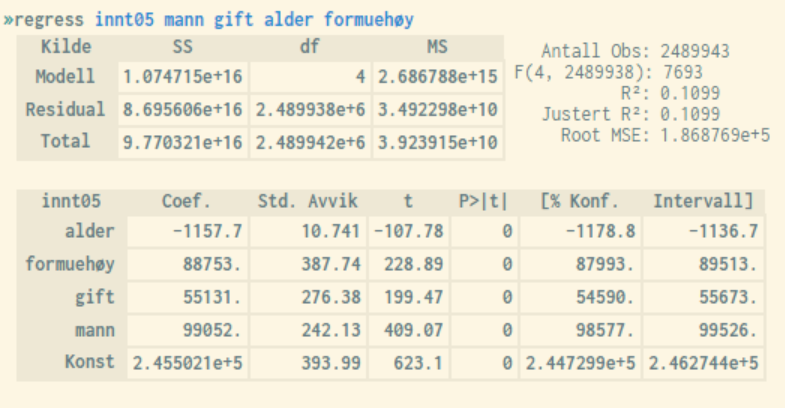
Justert gir et samlemål for hvor mye av den observerte variansen i den avhengige variabelen som kan forklares av summen av de uavhengige variablene. Skalaen går fra 0 til 1, der nærmest mulig 1 er det ideelle. I praksis vil en aldri nå verdien 1 ved analyser av sosioøkonomiske individdata pga. tilfeldig støy og uobserverte årsakssammenhenger, og typiske verdier vil gjerne ligge i intervallet 0 - 0.5.
vil alltid øke i verdi for hver ekstra uavhengige variabel som legges til. Dette betyr ikke nødvendigvis at modellen blir bedre, spesielt om variablene en legger til ikke er signifikante. Justert tar hensyn til dette og vil kun øke i verdi dersom de ekstra variablene er signifikante.
Dersom Justert får lavere verdi ved å tilføye en ekstra uavhengig variabel, er dette en indikasjon på den valgte variabelen kan ha en relativt høy grad av korrelasjon med noen av de andre uavhengige variablene, dvs. multikollinearitet. Dette er absolutt noe en bør unngå.
"P > |t|" eller p-verdiene (i kolonne 4 i den nedre hovedtabellen) angir sannsynligheten for at t-verdien fremkommer som et resultat av ren tilfeldighet. For å kunne si at en variabel er signifikant, må den tilhørende p-verdien være lavere enn 0.05 ved et 5%-signifikansniv�å. Verdier nærmest mulig 0 er ideelt.
Verdien t (kolonne 3) er kort fortalt et standardisert mål for koeffisientverdien (=marginaleffekten), jfr. verdiene i Coef.-kolonnen (kolonne 1), der en ved et 5%-signifikansnivå får grenseverdier på +/- 1.96. Verdier som overstiger 1.96 med positivt eller negativt fortegn vil altså regnes som signifikante på et 5%-nivå (5%-nivå er den grenseverdien som er vanlig å operere med).
En kan også se på 95%-konfidensintervallet presentert i de to kolonnene lengst til høyre i hovedtabellen. Dersom intervallet inkluderer verdien 0, kan en utelukke at den aktuelle koeffisienten viser en signifikant sammenheng mellom den tilhørende uavhengige variabelen og responsvariabelen.
Koeffisientverdiene i kolonne 1 er kun relevante for signifikante variabler, og viser marginaleffekten på responsvariabelen av en enhets økning i verdien på den tilhørende uavhengige variabelen.
I eksempelet ovenfor ser en at alle variablene er signifikante med god margin (høye t-verdier). Alder har negativ effekt på inntekt, mens de øvrige variabler har positiv effekt. "Konst" peker på konstantleddet, dvs. startverdien på responsvariabelen når alle uavhengige variabler har verdien 0, og har ikke noen stor betydning rent tolkningsmessig.