Ny analysefunksjonalitet: Regression Discontinuity Design

Regression Discontinuity Design (RDD) er en statistisk metode som brukes til å estimere kausal effekt i situasjoner der en behandling eller intervensjon er tildelt basert på en bestemt terskel eller kutt-punkt i en kontinuerlig variabel.

Modellen kan ses på som en spesiell variant av regresjonsanalyse, der man har en klart definert hypotese/antakelse om at en gitt hendelse skjer dersom man kommer over en terskelverdi for en spesifisert cutoff-variabel (også kalt «running variable»), og som gjør at den avhengige variabelen gjør et hopp enten opp (positivt estimat) eller ned (negativt estimat). Cutoff-variabelen bør helst være kontinuerlig, men også variabler med rangerbare numeriske verdier kan brukes.

I praksis estimeres to separate regresjonskurver, én for populasjonen med verdi på cutoff-variabelen som er lavere enn cutoff-punktet, og en annen for gruppen som har verdi høyere enn cutoff-grensen. Estimatene som rapporteres i hovedtabellen etter kjøring av kommando svarer til den vertikale avstanden mellom de to regresjonskurvene målt ved cutoff-punktet.

Illustrasjon av case som passer til RDD-analyse:

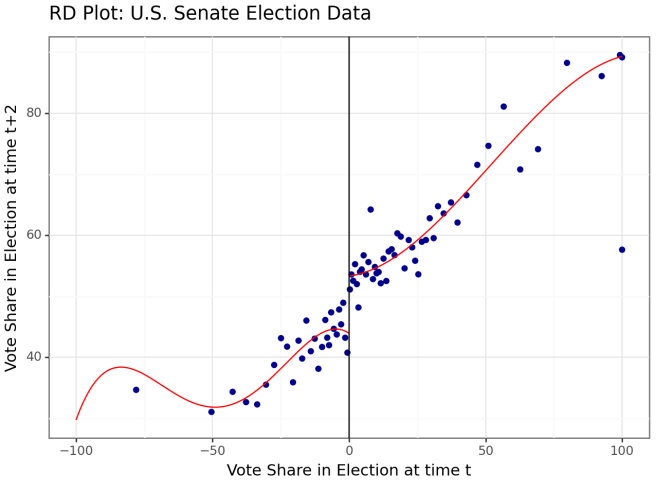
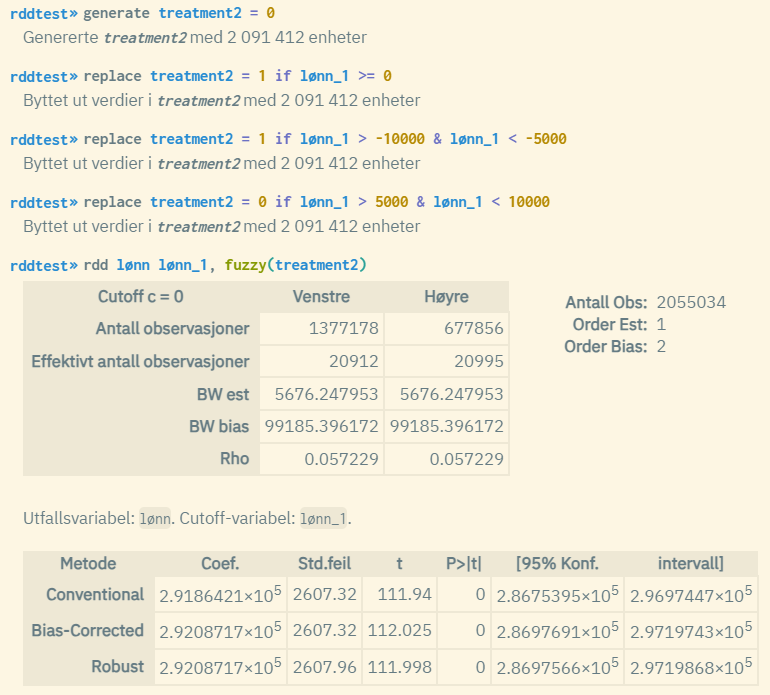
Denne analysen ser på effekten av å vinne et valg (margin > 0) på valgresultatet to år senere. Man ser tydelig at plottene gjør et vertikalt hopp når man får en positiv margin, dvs. passerer nullpunktet (altså man vinner valget). Kilde: Calonico, Cattaneo & Titiunik. https://rdpackages.github.io/rdrobust/

Regresjonskommandoen rdd kjører som standard en såkalt «Sharp Robust RDD», dvs. at det er en deterministisk sammenheng. Dersom man i stedet har en antakelse om at det er en gitt sannsynlighet for at behandling/intervensjon skjer etter cutoff-punktet (sannsynlighet lavere enn 100%), kan man gjennom opsjonen fuzzy() kjøre en «Fuzzy Robust RDD». Dette krever at man lager en såkalt treatment-dummy som tar verdien 1 dersom behandling/intervensjon, og 0 ellers. Denne dummyen angis som argument inni fuzzy()-opsjonen.

Felles for begge variantene «Sharp» og «Fuzzy» er at man må angi minst to variabler i rdd-uttrykket: Den første variabelen (avhengig variabel) kan være av valgfritt numerisk format, mens variabel nr. 2 (cutoff-variabel / running variable) må være enten kontinuerlig eller rangerbar. Øvrige forklaringsvariabler angis som variabel nr. 3 og utover. Cutoff-punktet er satt til verdien 0 som standard, gitt ved variabel nr. 2. Dette kan justeres gjennom opsjonen cutoff(). Ellers har man også opsjonene polynomial(), derivate(), level() og cluster() som man kan bruke til å gjøre visse justeringer i estimeringen. For info om disse bruk kommandoen help rdd i analysemiljøet.

Kommandoen hexbin er et nyttig hjelperedskap for å se hvorvidt man kan observere en vertikal forskyvning av observasjonene for din populasjon, noe som gir en pekepinn hvorvidt RDD-modellen din er godt egnet til å teste dine hypoteser. Man kjører da hexbin med hhv. avhengig variabel og cutoff-variabel som argument, og får da ut et anonymisert spredningsplott der man kan observere om det skjer noe systematisk før/etter cutoff-punktet.

Eksempel 1: Sharp RDD

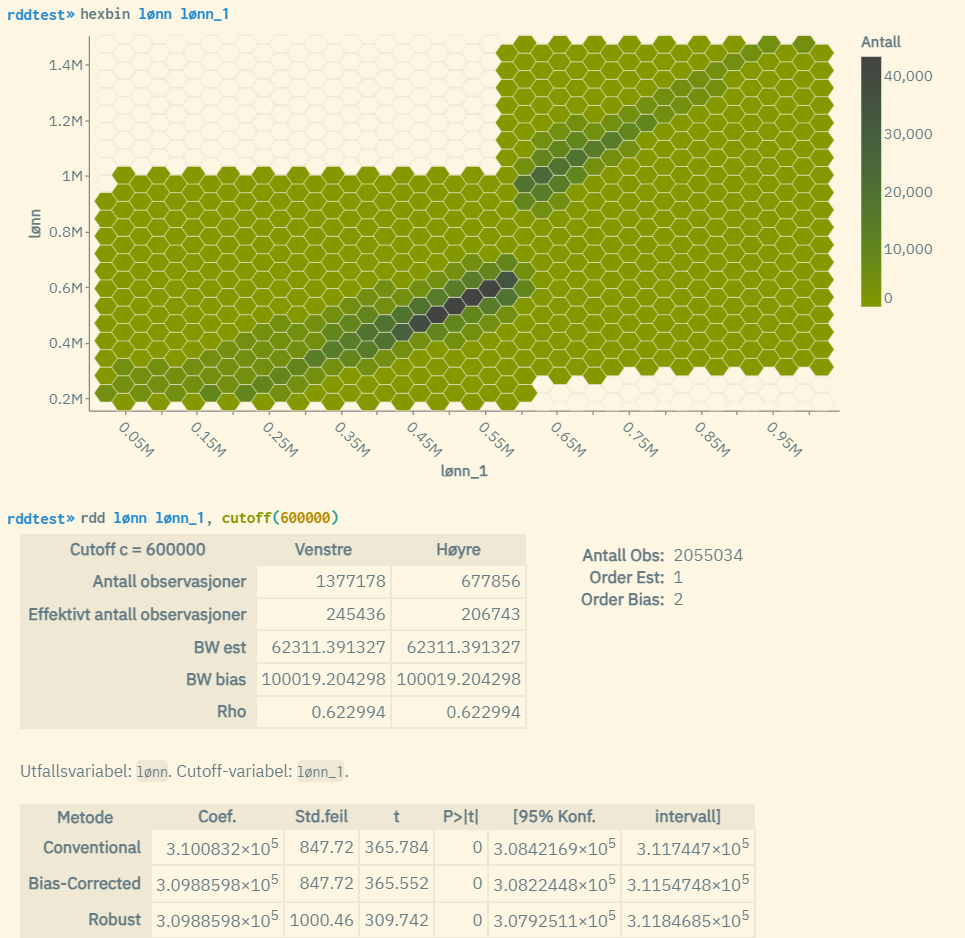
Hexbin-grafen viser et case der man har en 100% deterministisk sammenheng. Man ser et tydelig hopp oppover i plottene (mørk farge indikerer sterk intensitet i plottforekomster) ved cutoff-verdien 600 000. Variablene «lønn» og «lønn_1» er årlig lønnsinntekt hhv. for et bestemt år og året før, der man har manipulert «lønn» ved å multiplisere med en faktor på 1.5 dersom lønn_1 >= 600000. I estimatene nederst kan man se av linjen «Conventional» at effekten av å nå en inntekt på 600 000 året før utgjør ca. 310 000. Og med en p-verdi lik 0, er resultatet svært signifikant.

I eksempelet over brukes cutoff-grenseverdien 600000 ettersom vi vet at det er ved dette punktet at man kan observere en forskyvning av regresjonslinjene. Om man ønsker, kan man standardisere verdiene til cutoff-variabelen «lønn_1» ved å trekke 600 000 fra alle verdier. Da vil cutoff-grenseverdien bli 0 i stedet, og man trenger ikke bruke opsjonen cutoff() siden 0 er standardvalget for rdd. Resultatene av rdd-kjøringen vil bli identiske.

Eksempel 2: Fuzzy RDD

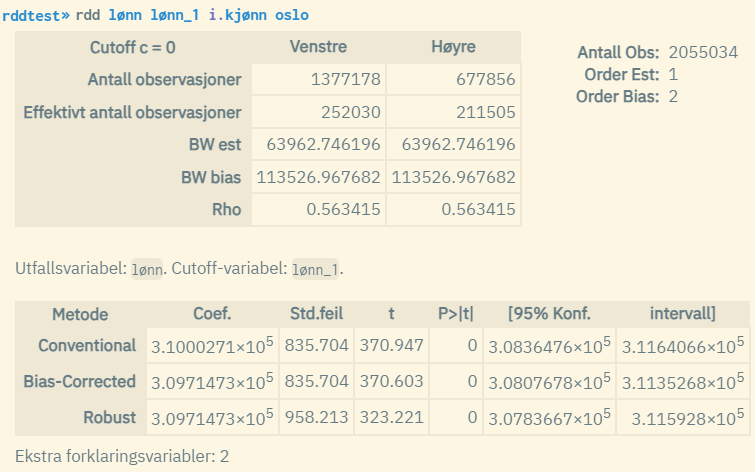
Her er cutoff-variabelen standardisert slik at cutoff-verdi = 0. I tillegg lages en «treatment»-variabel som tar verdiene 0 eller 1 både før og etter cutoff-punktet. Da har man en ikke-deterministisk sammenheng der en fuzzy-modell er mer passende å bruke. Også her blir p-verdiene lik 0, noe som er en indikasjon på god «modell-fit».

Eksempel 3: Sharp RDD med ekstra forklaringsvariabler

I dette caset bruker man også forklaringsvariablene «kjønn» (faktorvariabel) og «oslo» (dummy). Dette får ikke så mye å si for estimatene for den vertikale forskyvningen. Merk at estimater for de ekstra forklaringsvariablene ikke vises i resultatet. Dette er standard måte å rapportere slike estimater på.

Om resultatene:

Conventional: Vanlig RD-estimat (estimat for vertikal forskyvning ved cutoff-punktet)
Bias-Corrected: Skjevhetsjustert RD-estimat med vanlige standardfeil
Robust: Skjevhetsjustert RD-estimat med robuste standardfeil

Effektivt antall observasjoner: Det antallet observasjoner som brukes til å estimere hhv. til venstre og høyre for cutoff-punktet (man bruker bare de nærmeste observasjonene ved estimering)
BW est: Dette angir grenseverdiene for hvilke observasjoner som benyttes i estimeringen av det vanlige RD-estimatet, altså cutoff-verdi +/- oppgitt verdi
BW bias: Angir grenseverdiene knyttet til estimeringen av den skjevhetsjusterte estimatoren, altså cutoff-verdi +/- oppgitt verdi
Rho: «BW est» dividert med «BW bias»
Order Est: Orden på den lokale polynomial som brukes til å estimere punktestimatoren (ved cutoff-punktet). Standardverdi er 1, men dette kan endres gjennom opsjonen polynomial(). Verdien 1 indikerer lokal lineær regresjon.
Order Bias: Orden på den lokale polynomial som brukes til å estimere skjevhetsjusteringen (ved cutoff-punktet). Standardverdi er 2, som indikerer lokal kvadratisk regresjon. Verdien justeres automatisk etter verdi på «Order Est».

Klikk her for lenke til skript som gjenskaper eksemplene over.

Kilde:

Algoritmene for kommandoen rdd bygger på Pythonkode utviklet av Calonico, Cattaneo, & Titiunik: https://github.com/rdpackages/rdrobust/tree/master/Python/rdrobust