Ny analysefunksjonalitet: Kaplan-Meier overlevelsesanalyse

Nå er det mulig å kjøre Kaplan-Meier overlevelsesanalyse i microdata.no. Kommandoen «kaplan-meier» er først ut i en serie av denne typen analyser. Etterhvert vil vi også introdusere multivariat cox-analyse.

Innen medisinsk forskning brukes overlevelsesanalyser ofte til analyser av sannsynligheten for overlevelse evt. død over tid. Det trenger ikke nødvendigvis være død i streng forstand, men også andre tilstander som syk etc. Innen samfunnsforskning er det mer vanlig å fokusere på tilstander som «arbeidsledig», «ufør» etc. Man kan altså bruke overlevelsesanalyser til å estimere sannsynligheter for å bli arbeidsledig, ufør eller annet over tid.

Kaplan-Meier
Dette er den enkleste og kanskje vanligste typen overlevelsesanalyse. Standardresultat fra en slik analyse er kaplan-meier-grafer som typisk viser en trappetrinnformet kurve som går nedover langs x-aksen (tid). Selve kurven viser overlevelsesraten som funksjon av tid, og er gitt ved følgende formel:

I tillegg til grafer vises også nøkkeltall for den aktuelle analysepopulasjonen. Kaplan-Meier kan også brukes til å lage bivariat analyse av overlevelsesraten der man ser på forskjeller mellom grupper av populasjonen. Dette gjøres gjennom bruk av en «by-opsjon» der man kan vise separate kurver for hver gruppe i en og samme graf.

Kaplan-Meier er en ikke-parametrisk analyseform for enkle overlevelsesanalyser, men kan også brukes som hjelpeverktøy for å sette opp mer avanserte analyser, f.eks. multivariate cox-analyser: Ved å studere kaplan-meier-grafer kan man sammenlikne overlevelsesratene for de ulike gruppene av individer man grupperer gjennom forklaringsvariabler, og se om det er signifikante forskjeller i overlevelsesraten mellom f.eks. kvinner og menn. Om kurvene ikke overlapper, er dette et tegn på at den aktuelle forklaringsvariabelen er god å benytte som forklaringsvariabel til en multivariat analyse.

Hvordan tilrettelegge data for overlevelsesanalyse

Overlevelsesanalyser krever følgende:

• En ferdig definert måleperiode
• En klar definisjon av hvilken hendelse man vil estimere sannsynligheten for
• Et ferdig tilrettelagt datasett som må inneholde følgende variabler:
  – Tid
  – Hendelse

Variabelen «tid» må inneholde et mål på tiden som har gått fra et gitt start-tidspunkt til den spesifikke hendelsen skjer. Man kan fritt velge måleenhet, f.eks. antall dager, uker, måneder eller år. Det eneste kravet er at «tid» må være en numerisk variabel.

Variabelen «hendelse» må også være numerisk og inneholde verdien 1 for personer hvor hendelsen faktisk har skjedd i løpet av den gitte måleperioden. For personer hvor hendelsen evt. ikke har skjedd i denne perioden, settes verdien til 0. Sistnevnte kalles «sensurerte» tilfeller. Dette er altså personer der man ikke kan vite om hendelsen har skjedd, enten for at den kan ha skjedd etter at måleperioden var ferdig, eller for at de har forsvunnet fra populasjonen i løpet av måleperioden. Man må ikke angi verdien 0, det kan ofte være tilfeller der «hendelse» har verdien 1 for alle enheter (individer).

Tid og hendelse kan beregnes gjennom bruk av import-kommandoen import-event (lar deg definere hendelsesvariabel og måleperiode, og legger til startdateringer for alle hendelser i ditt datasett) samt aggregeringskommandoen collapse(min) (brukes på startdateringsvariabelen for å finne tidspunktet for den gitte hendelsen gitt ved en spesifikk verdi på variabelen du importerer gjennom import-event). Det er også mulig å benytte ferdige dateringsvariabler med faste verdier per enhet.

Klikk her for full gjennomgang av fremgangsmåter for å sette opp et datasett for tidsserieanalyse.

Selve analysen

Etter at du har datasettet ditt klart for overlevelsesanalyse, jfr. avsnittet over, kan du kjøre en kaplan-meier-analyse gjennom å bruke kommandoen kaplan-meier der man først angir variabelen «hendelse» og deretter «tid» (rekkefølgen er viktig). Eksempler:

kaplan-meier hendelse år
kaplan-meier hendelse dager
kaplan-meier hendelse år, by(kjønn)
kaplan-meier hendelse dager, by(aldersgruppe)

Typisk resultat fra en slik kommando:

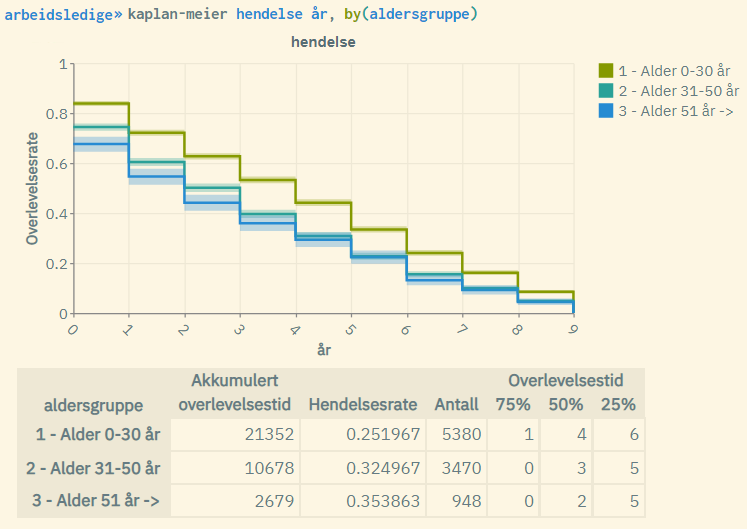
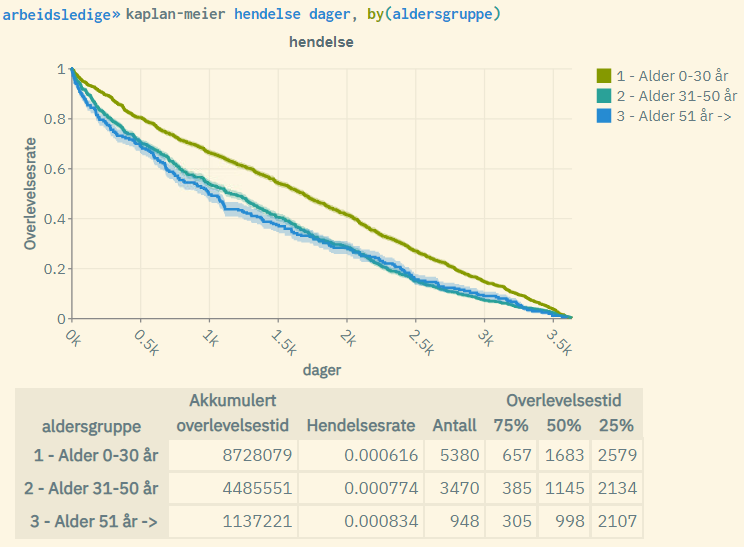
Forklaring til figuren:

• Kurvene er gitt ved kaplan-meier-formelen for hver av aldergruppene. De yngste kommer best ut med en høyere «overlevelsesgrad» (blir i mindre grad arbeidsledige over tid)
• De skraverte områdene representerer standard log-log 5% konfidensintervall tilknyttet overlevelsesraten for hver av aldersgruppene. Disse vil være mindre synlig ved store populasjoner.
• «Akkumulert overlevelsestid»: Summen av tid målt over alle enheter i populasjonen (innen hver aldergruppe).
• «Hendelsesrate»: Antall hendelser inntruffet (antall enheter med hendelse = 1) dividert med «akkumulert overlevelsestid».
• «Antall»: Antall enheter (for hver av aldersgruppene)
• «75%»: Tid målt der hvor overlevelsesraten = 0.75 (for hver av aldergruppene)
• «50%»: Tid målt der hvor overlevelsesraten = 0.5 (for hver av aldersgruppene). Også kalt «median overlevelsestid»
• «25%»: Tid målt der hvor overlevelsesraten = 0.25 (for hver av aldersgruppene)