It is now possible to display standardized regression estimates

The new option standardize allows you to display standardized coefficient estimates when using the regress (OLS estimation) command.

Comparison of coefficient estimates for the various explanatory variables in a regression model will be challenging if they use different value scales. It then becomes difficult to see which variables have the strongest effect on the response variable.

Standardization takes place by all the variables included in a regression model, including the response variable, being rescaled to a standardized distribution with expectation equal to 0 and variance equal to 1. This makes the estimates directly comparable both within and across different regression models.

Standardized coefficients show how many standard deviations the response variable will change if the relevant explanatory variable increases by one standard deviation.

Displaying standardized estimates for linear regression is easily done by using the standardize option together with the regress command.

The example below shows results from OLS regression run on the same data, first the regular variant and then the standardized variant. Note that the model values in the upper part of the results relate to the estimation on common unstandardized data, which makes the numbers equal. The bottom part showing the coefficient estimates, on the other hand, will be different with the exception of the t and P values. Note also that no standardized estimate is reported for the constant term when the standardize option is used.

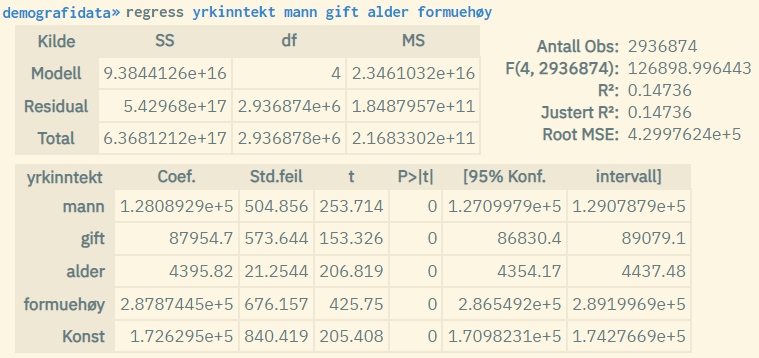
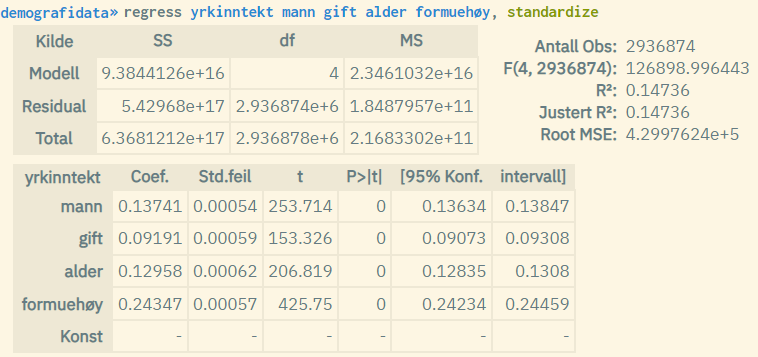
Standard OLS estimation using regress command

Standardized OLS estimation using regress command with standardize-option

In microdata.no, we have chosen to post-standardize the coefficient estimates using the following formulas (gives the same result as using standard regression on pre-standardized data):

Standardized coefficients: Coef^∗ = Coef · (sd(x) / sd(y)) , where Coef = unstandardized coefficient, sd(x) = standard deviation of independent variable measured over the current population, sd(y) = standard deviation of dependent variable measured over the current population

Standardized standard errors: Std.error^*= Coef^* / t (equivalent to Std.error^* = Std.error · (sd(x) / sd(y)))

Standardized confidence interval (95%): CI^* = [Coef^* − 1.96 · Std.error^* ; Coef^* + 1.96 · Std.error^*] (the parameter 1.96 corresponds to the default level 95%)